Problem Statement

高尔夫球是一种在上流社会非常流行的运动。

高尔夫球场可以被抽象为一个二维平面。高尔夫球初始时位于 $(S_X,S_Y)$，而球洞位于 $(T_X,T_Y)$。

高尔夫球场中有许多矩形障碍物。具体地，一共有 $n$ 个障碍物，其中第 $i$ 个可以被抽象为一个左下角位于 $(L_i,D_i)$，右上角位于 $(R_i,U_i)$ 的矩形。保证起点和终点都不在障碍物的内部以及边界上。

为了降低难度，本题中的击球仅允许向上、下、左、右四个方向击球（即必须平行于 $x$ 轴或者 $y$ 轴）。击球后，球会沿着击球方向运动。我们假设击球者水平很高，可以让球在经过的任意整点停下来。但是，球的路径不能经过障碍物内部（沿着障碍物的边界运动是允许的）。

求最少要击球多少次，才可以把球打进 $(T_X,T_Y)$。本题中，我们假设球一旦经过球洞所在的位置，它就会掉下去。

Input

第一行四个空格隔开的整数 $S_X,S_Y,T_X,T_Y$，表示高尔夫球的初始位置以及球洞的位置。

第二行一个整数 $n$，表示障碍物的个数。

接下来 $n$ 行，每行四个空格隔开的整数 $L_i,R_i,D_i,U_i$，描述一个障碍物。

Output

输出仅有一行一个整数，表示最少的击球次数。容易发现一定存在至少一种击球方案，使得球可以进洞。

Sample Input

2 15 20 19
1
8 19 12 20

Sample Output

3

Sample Explanation

如图，不难发现 $2$ 次击球一定不可行。

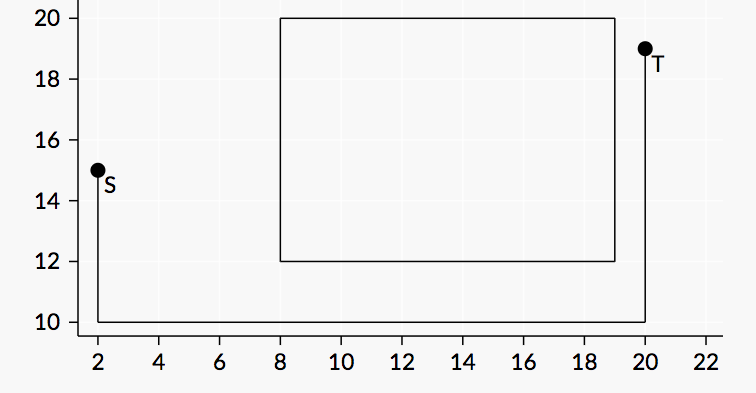
$3$ 次击球的一条最优路径是：$(2,15)\to (2,10)\to (20,10)\to (20,19)$。

Constraints

对于所有数据，$0\le n\le 10^5$，$1\le L_i\lt R_i\le 10^9$，$1\le D_i\lt U_i\le 10^9$，$1\le S_X,S_Y,T_X,T_Y\le 10^9$，保证 $(S_X,S_Y)\ne (T_X,T_Y)$，且 $(S_X,S_Y),(T_X,T_Y)$ 均不在任何障碍物的内部以及边界上，任意两个障碍物（包括边界）互不相交。

• Subtask $1$（$\ \ 5\%$）：$n=0$；
• Subtask $2$（$15\%$）：$n\le 10$；
• Subtask $3$（$15\%$）：$n\le 100$，所有坐标范围不超过 $100$；
• Subtask $4$（$15\%$）：$n\le 1000$，所有坐标范围不超过 $1000$；
• Subtask $5$（$15\%$）：$n\le 1000$；
• Subtask $6$（$35\%$）：无特殊限制。

时间限制：$5\texttt{s}$

空间限制：$512\texttt{MB}$